
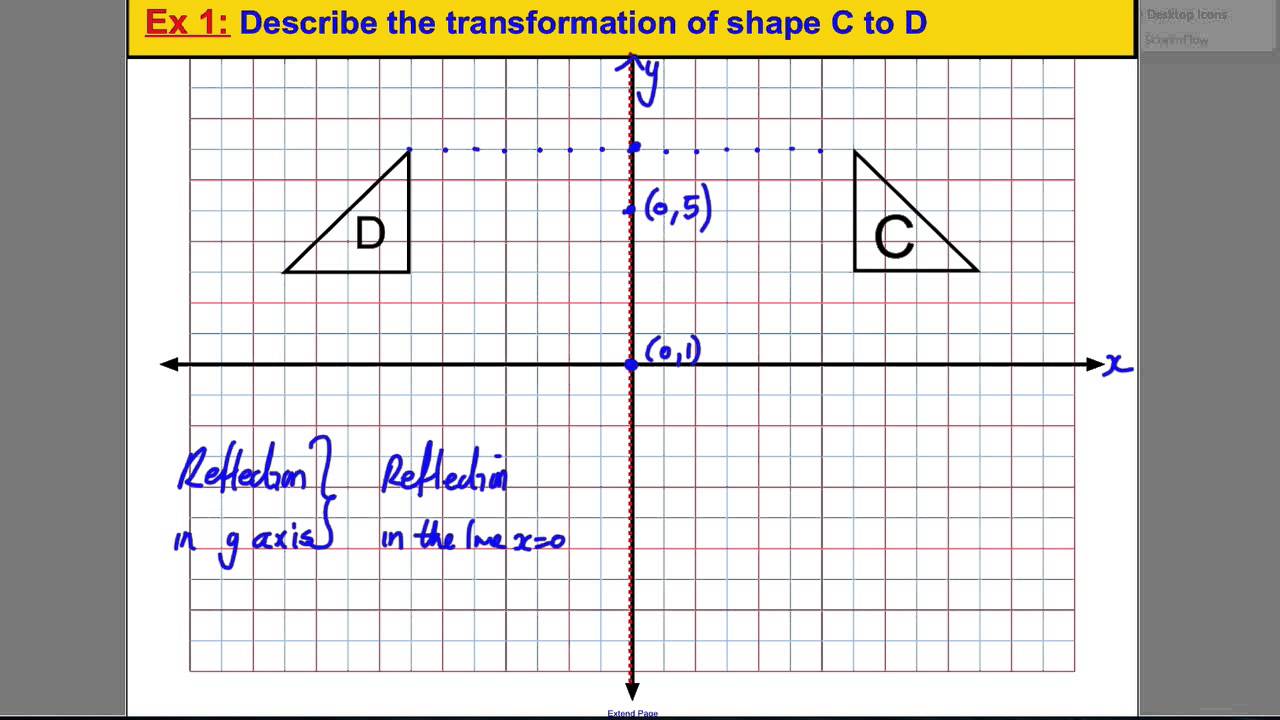
The shape rotates counter-clockwise when the number of degrees is positive and rotates clockwise when the number of degrees is negative. The transformation that rotates each point in the shape at a certain number of degrees around that point is called rotation. The transformation of f(x) is g(x) = - x 3 that is the reflection of the f(x) about the x-axis. Here is the graph of a quadratic function that shows the transformation of reflection. Thus the line of reflection acts as a perpendicular bisector between the corresponding points of the image and the pre-image. If point A is 3 units away from the line of reflection to the right of the line, then point A' will be 3 units away from the line of reflection to the left of the line. Every point (p,q) is reflected onto an image point (q,p). When the points are reflected over a line, the image is at the same distance from the line as the pre-image but on the other side of the line. The type of transformation that occurs when each point in the shape is reflected over a line is called the reflection. The transformation f(x) = (x+2) 2 shifts the parabola 2 steps right. This pre-image in the first function shows the function f(x) = x 2. We can apply the transformation rules to graphs of quadratic functions. This translation can algebraically be translated as 8 units left and 3 units down.
Translation of a 2-d shape causes sliding of that shape. Transformations help us visualize and learn the equations in algebra. We can use the formula of transformations in graphical functions to obtain the graph just by transforming the basic or the parent function, and thereby move the graph around, rather than tabulating the coordinate values. Transformations are commonly found in algebraic functions. Transformations can be represented algebraically and graphically. Here are the rules for transformations of function that could be applied to the graphs of functions.

On a coordinate grid, we use the x-axis and y-axis to measure the movement. Columbia University.Consider a function f(x). “Private tutoring and its impact on students' academic achievement, formal schooling, and educational inequality in Korea.” Unpublished doctoral thesis.
#Transformation and reflection graph professional
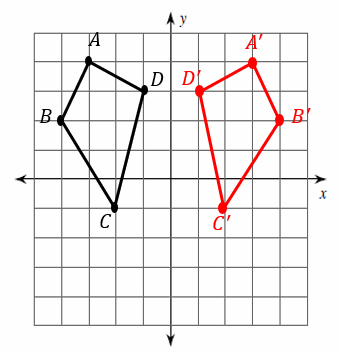
Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage. Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20. This dilation can be described in coordinate notation as The figure below shows a dilation with scale factor Of a dilation is the factor by which each linear measure of the figure (for example, a side length) is multiplied. Is a transformation which preserves the shape and orientation of the figure, but changes its size. (Again, you can check this by plugging in the coordinates of each vertex.) This reflection can be described in coordinate notation as (You can check that this works by plugging in the coordinates This rotation can be described in coordinate notation as This translation can be described in coordinate notation as For example, in the figure below, triangle , is not isometric: it preserves the shape of the figure but not its size. Means that the transformation doesn't change the size or shape of the figure.) A fourth type of transformation, a dimensional shapes: translations, rotations, and reflections.


 0 kommentar(er)
0 kommentar(er)
